グラフィックスの変形
グラフィックスの変形に関しては、図形を回転させたいのであればrotateメソッド、図形を移動させたいのであればtranslateメソッド、図形を倍率変換したいのであればscaleメソッドを用います。これらの引数は以下の通りです。
また、rotateメソッドはキャンバスの左上を基準として回転し、scaleメソッドも同じように左上を基準として図形を伸縮させます。
// 画像の回転 rotate(angle); // 画像の移動 translate(x, y); // 画像の伸縮 scale(x, y);
また、上記のメソッドの動作を1つのメソッドで行えるものがあり、それがtransformメソッドです。引数は以下の通りです。
// transformメソッド transform(m11, m12, m21, m22, dx, dy); // 単位マトリックス transform(1, 0, 0, 1, 0, 0); // 新たな変換マトリックスを定義 setTransform(m11, m12, m21, m22, dx, dy);
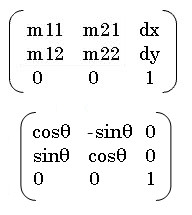
変換マトリックス(変換行列)は平面上の点を別の点に変換します。transfromメソッドの各値は右の行列式の各値に当たり、現在の座標を(x, y)、変換後の座標を(x', y')とした場合、以下のような式で表わされます。なお、右の行列式の第3行目の値は(0 0 1)で固定となっています。
- x' = m11*x + m21*y + dx
- y' = m22*y + m12*x + dy
dx,dyは水平、垂直方向の平行移動を表します。よって平行移動はdx,dyを設定することで行われます。
m11,m22は水平、垂直方向のスケーリングを表します。よってスケーリングはm11,m22を設定することによって行われます。例えばm11を5、m22を2に設定すると、高さが5倍で幅が2倍となります。
m12,m21は水平、垂直方向のシャーリング(傾き)を表します。よってシャーリングはm12,m21を設定することによって行われます。m12,m21を0以外の値に設定すると、座標系が歪みます。
回転に関しては、スケーリングとシャーリングを調整することによって行うことができます。
ここで、単位マトリックスは、m11とm22が1、m12とm21が0のものです。右の下の行列式は、平面上の点の回転移動をするための変換行列で、θが回転の角度を表わしています。単位マトリックスは角度が0なので代入すると、cosθがそれぞれ1、sinθと-sinθがそれぞれ0になるので、単位マトリックスと等しいと分かります。
transformメソッドで変換マトリックスを定義した後、別のtransformメソッドを定義すると、2つの変換マトリックスを掛け合わせた変換マトリックスが適用されます。つまりtransformメソッドはリセットしない限り、基準はその前のものに依存してしまいます。そこで、新たな変換マトリックスを定義するためには、setTransformメソッドを用います。
transformメソッド多少理解し辛い部分がありますが、以下のページを参考にすると理解しやすくなると思います。
サンプル
サンプルはすべてfor文を用いて表現しています。これによって各メソッドが引き継がれていく、ということが分かります。
まずrotateメソッドですが、基準の赤い丸を40度回転させました。またキャンバスの左上まで直線を描いたことで、キャンバスの左上を基準として回転しているということが分かります。
次にtranslateメソッドですが、幅と高さが共に40pxの四角形を、(25,25)程度ずらします。for文によって3回繰り返されていますが、translateメソッドで指定した値が引き継がれているので、四角形が以前の四角形より(25,25)ずれて表示されています。
scaleメソッドは、サンプルでは縦横ともに1.5倍しています。緑の円形は赤の円形の1.5倍となっており、青の円形は緑の円形の1.5倍となっています。また図形の伸縮は図形の左上を基準に行われることが、このサンプルから分かります。
最後のサンプルはtransformメソッドを用いたものです。for文の2重ループとtransformメソッドを組み合わせて表現されています。単純な変形であればrotateメソッド、translateメソッド、scaleメソッドで十分ですが、より複雑な変形に関してはこのtransformメソッドが合っていると言えます。
// 線の太さの設定
cx.lineWidth = 2;
// 色の定義(左から赤、青)
var color = ["rgba(256, 80, 80, 0.6)",
"rgba(80, 256, 80, 0.6)", "rgba(80, 80, 256, 0.6)"];
// 図形の描画と回転
for(i=0; i<2; i++){
// 円形の描画
cx.beginPath();
cx.arc(90, 40, 20, 0, 2*Math.PI, false);
cx.strokeStyle = color[i];
cx.stroke();
// キャンバスの左上までの線
cx.beginPath();
cx.moveTo(90, 40);
cx.lineTo(0, 0);
cx.strokeStyle = "rgb(150, 150, 150)";
cx.stroke();
// 図形を40度回転
cx.rotate(40 * Math.PI / 180);
}
// 変換マトリックスのリセット
cx.setTransform(1, 0, 0, 1, 0, 0);
// 文字の挿入
cx.fillText("rotateメソッド", 80, 80);
// 線の太さの設定
cx.lineWidth = 2;
// 色の定義(左から赤、青)
var color = ["rgba(256, 80, 80, 0.6)",
"rgba(80, 256, 80, 0.6)", "rgba(80, 80, 256, 0.6)"];
// 図形の描画とtranslateメソッドによる移動
for(i=0; i<3; i++){
cx.strokeStyle = color[i];
cx.strokeRect(50, 50, 40, 40);
// 図形の移動
cx.translate(25, 25);
}
// 変換マトリックスのリセット
cx.setTransform(1, 0, 0, 1, 0, 0);
// 文字の挿入
cx.fillText("translateメソッド", 100, 60);
// 線の太さの設定
cx.lineWidth = 2;
// 色の定義(左から赤、青)
var color = ["rgba(256, 80, 80, 0.6)",
"rgba(80, 256, 80, 0.6)", "rgba(80, 80, 256, 0.6)"];
// 図形の描画とscaleメソッドによる伸縮
for(i=0; i<3; i++){
cx.beginPath();
cx.arc(30, 50, 20, 0, 2*Math.PI, false);
cx.strokeStyle = color[i];
cx.stroke();
// 図形の伸縮
cx.scale(1.5,1.5);
}
// 変換マトリックスのリセット
cx.setTransform(1, 0, 0, 1, 0, 0);
// 文字の挿入
cx.fillText("scaleメソッド", 100, 50);
// 線の太さの設定
cx.lineWidth = 2;
// 色の定義(左から赤、青)
var color = ["rgba(256, 80, 80, 0.6)",
"rgba(80, 256, 80, 0.6)", "rgba(80, 80, 256, 0.6)"];
// 図形の描画とtransformメソッドによる変形
for(i=1; i<=10; i++){
var r_color = 25*i;
cx.strokeStyle = "rgb("+r_color+", 150, 230)";
for(j=0; j<10; j++){
cx.transform(1.0, 0, 0, 1.0, 3, 3);
cx.strokeRect(40, 30, 20, 20);
}
cx.setTransform(1,0,0,1,20*i,3*i);
}
// 変換マトリックスのリセット
cx.setTransform(1, 0, 0, 1, 0, 0);
// 文字の挿入
cx.fillText("transformメソッド", 100, 30);